公式推导好看，数值计算好用。
上溢和下溢
数学推导是美的，连续函数是理想的，计算机却做不到完美，随机函数不随机，有限数位有误差。当操作复杂时，即使理论可行，也可能由于程序中没有考虑误差的累积而导致算法失效。上溢（overflow）是指数值过大近似为无限，进一步计算通常会成为非数字（not-a-number，NaN），下溢（underflow）则是指数值接近零而被四舍五入为零，因而会在除法等运算中成为非数字。
上述两种溢出对于程序都是毁灭性的，我们需要在程序中保持数值稳定，一个典型的例子如softmax函数，其定义为\(softmax(x)_i = \frac{exp(x_i)}{\sum_{j=1}^n exp(x_j)}\)，我们考虑\(exp(c)\)，当\(c\)为很小的负数时会发生下溢，当\(c\)为很大的正数时会发生上溢。这时可利用\(softmax(z)\)来解决，其中\(z=x-max_i x_i\)，所以\(exp\)的最大参数是0，就排除了上溢的可能性，同时分母中至少有一个1，也就排除了因分母下溢而被零除的可能性，但依然要注意分子下溢的情况，这就需要另外的函数，也可以使用相同的技巧来稳定数值。
在实际应用中，我们可能无法时时检查或防备自己的程序出现数值溢出的情况，所以要尽量选择靠谱的底层库来帮助我们检测并保持数值稳定。
病态条件
另一种情况是输入的扰动，科学计算中往往并不希望输入的轻微扰动导致函数值的迅速改变，我们考虑条件数的概念，即对于\(f(x)=A^{-1}x\)，当\(A \in R^{n \times n}\)具有特征值分解时，其条件数为\(max\vert \frac{\lambda_i}{\lambda_j}\vert\)，即最大和最小特征值的模的比值。该数越大，则矩阵求逆对输入的扰动就越敏感。由于这是矩阵本身的固有特性，我们称之为病态条件，故在实际应用中需谨慎考虑其对于数值误差的放大效果。
基于梯度的优化方法
大多数机器学习算法都涉及到某种形式的优化，即通过改变\(x\)而最小化或最大化目标函数\(f(x)\)，常见的如最小化损失函数（loss function），这里我们记为\(x^*=arg\ min f(x)\)。
复习一点儿导数（derivative）的知识，对于实数域函数\(y=f(x)\)，其导数记为\(f'(x)\)或\(\frac{dy}{dx}\)，代表着原函数在该点处的斜率，可以有\(f(x+\epsilon) \approx f(x)+\epsilon f'(x)\)。因此导数对于最小化一个函数十分有用，因为我们可以将\(x\)往导数的反方向移动一小步而减小\(f(x)\)，这种方法就被称为梯度下降（gradient descent），如下图的例子：
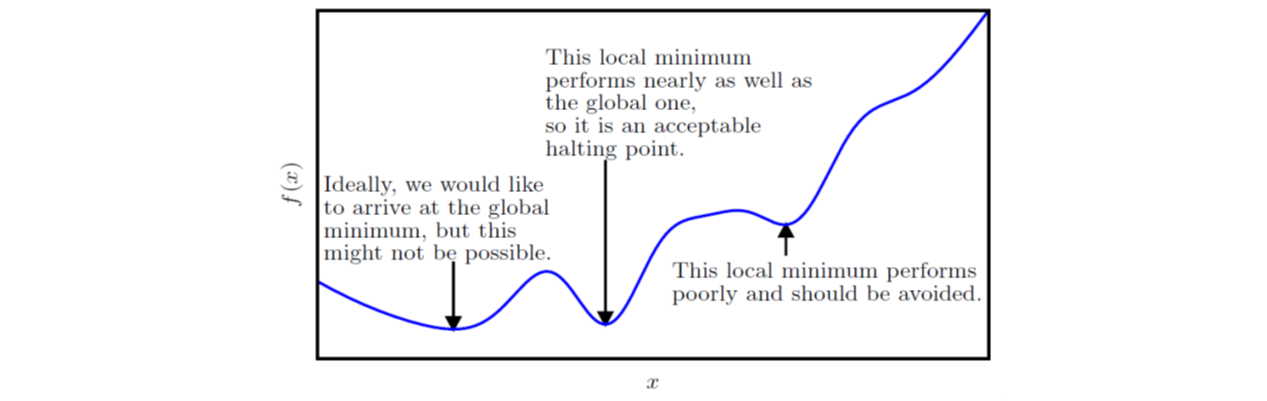
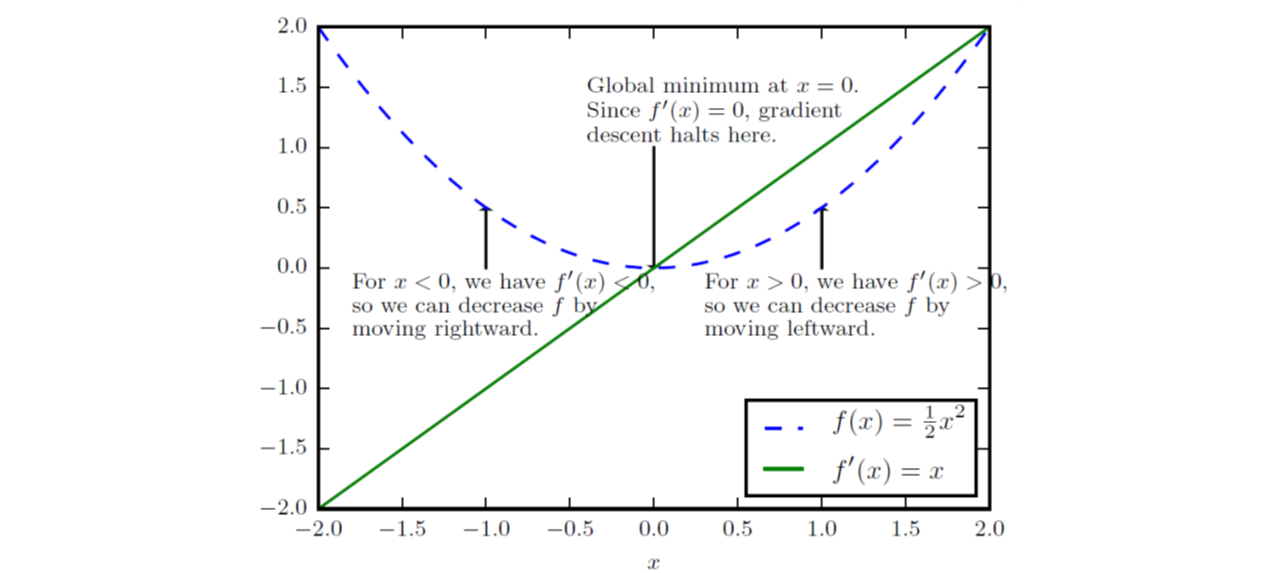实际应用中，一个函数可能存在多个全局最小点，可能存在不是全局最优的局部极小点，还可能有很多处于平坦区域内的鞍点，这让优化工作变得困难，通常会变成一个性价比的选择问题，比如下图：
更多的时候，我们的输入是多维的，这时就会用到偏导数（partial derivative），即\(\frac{\vartheta}{\vartheta x_i}f(x)\)，其衡量了点\(x\)处只有\(x_i\)变化时\(f(x)\)的变化情况。这里的梯度就是包含所有偏导数的向量，记为\(\nabla_x f(x)\)。这时，我们定义一个方向导数（directional derivative），其为函数\(f\)在单位向量\(u\)方向的斜率，有\(\frac{\vartheta}{\vartheta \alpha}f(x+\alpha u)=u^T \nabla_x f(x)\)，为了最小化\(f\)，则有：
可以看到在负梯度方向上移动能够减小\(f\)，即为梯度下降。还可以设置\(\epsilon\)为学习率（learning rate），用于确定每一步下降的步长，\(x'=x-\epsilon\nabla_x f(x)\)。\(\epsilon\)可设置为常数，也可线搜索等。同时，梯度下降的思想还可扩展到离散空间中，比如有爬山算法（hill climbing）等。
有时候我们希望进一步考察函数曲率的变化，衡量梯度下降的表现，确定一个临界点是否是局部极大点、局部极小点或鞍点等，这就需要二阶导数，相应地，对于多维输入有Hessian矩阵，其等价于梯度的Jacobian矩阵。仅使用梯度信息的优化算法被称为一阶优化算法（first-order optimization algorithms），如梯度下降。使用Hessian矩阵的优化算法被称为二阶最优化算法（second-order optimization algorithms），如牛顿法。
约束优化
有些时候，我们希望\(x\)在某些集合\(S\)中找到\(f(x)\)的最大/最小值，这被称为约束优化（constrained optimization），此时集合\(S\)中的点称为可行（feasible）点。
一个简单的解决方法时将约束考虑在内后简单地对梯度下降进行修改，即将每次下降的点映射回\(S\)。一个复杂的方法是设计一个不同的、无约束的优化问题，令其解可以转化成原始约束优化问题的解，例如，我们要在\(x \in R^2\)中最小化\(f(x)\)，其中\(x\)被约束为需要具有单位\(L^2\)范数，这时，我们可以设置关于\(\theta\)的函数\(g(\theta)=f([cos\theta, sin\theta]^T)\)，令其最小化，最后返回\([cos\theta, sin\theta]\)作为原问题的解。这种方法需要创造性，可能需要根据每一种情况分别进行设计，Karush–Kuhn–Tucker方法是一个针对约束优化的通用解决方案，具体的还是细查文献吧。
实例：线性最小二乘
假设我们希望找到最小化下式的\(x\)的值：
\[f(x) = \frac{1}{2} \|Ax-b\|_2^2\]利用梯度下降算法，首先计算梯度：
\[\nabla_x f(x) = A^T(Ax-b) = A^TAx-A^Tb\]然后设置步长（\(\epsilon\)）和容差（\(\delta\)）为小的正数，伪代码如下：
\[while\ \| A^TAx-A^Tb \|_2 > \delta\ do \\ \ \ \ \ x \leftarrow x - \epsilon(A^TAx-A^Tb) \\ end\ while\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\]其它的算法还有牛顿法、Lagrangian等。
