一切都是随机事件,听天由命吧~
为什么要使用概率?
人有大概率犯傻,机器却小概率犯错,这也许是人工智能一直“不像人”的片面原因。概率论和信息论是现代工业最重要的学科,几乎所有的人类活动都面临着在不确定的情况下进行推理的需求,究其原因大抵这三种:观察的不完全性、模型的不完全性、系统的内部随机性。
实现一个完全的、确定的系统过于复杂,在实际生活中,简单模糊的规则往往更实用,这即是以不确定性来进行表示和推理。概率学派常分为两种:频率派概率(frequentist probability) 和贝叶斯概率(Bayesian probability),两派争吵不休,一方基于反复试验,另一方则认为事件可能互相影响。其实不存在谁的绝对正确,只是哲学思想的不同罢了。
随机变量和概率分布
概率论和信息论提供了形式化规则,方便计算机程序化实现。随机变量(random variable)即指随机取值的变量,可以是离散的,也可以是连续的。概率分布(probability distribution)则描述了随机变量在每个一状态(取值)的可能性大小。
离散型变量的概率分布是概率质量函数(probability mass function,PMF),连续型变量则用概率密度函数(probability density function,PDF)来表示,它们需要具有以下几个条件:
- \(p\)的定义域是\(x\)所有状态的集合
- \(\forall x,p(x) \ge 0\),对于PMF,则还要求\(p(x) \le 1\)
- \(\int p(x)dx = 1\)(对于连续型变量,需要用微积分的观点来看待)
另外,对于多个随机变量,我们使用联合概率分布(joint probability distribution)来表示。当我们需要知道一组变量子集的概率分布时,即边缘概率分布(marginal probability distribution),可用积分(求和):\(p(x) = \int p(x,y)dy\)。
条件概率
更多的时候,我们感兴趣的是某个事件在有其它事件发生时的概率,即条件概率(conditional probability),比如在x发生时y的概率,可以用下述公式计算:
\[P(y\vert x)=\frac{P(y,x)}{P(x)}\]条件概率具有链式法则(chain rule),可以把任意多维随机变量的联合概率分布,分解为只有一个变量的条件概率相乘的形式:
\[P(x^{(1)},...,x^{(n)})=P(x^{(1)})\prod_{i=2}^n P(x^{(i)}\vert x^{(1)},...,x^{(i-1)})\]另外,对于两个随机变量\(x\)和\(y\),如果存在\(P(x,y)=P(x)P(y)\),则称这两个随机变量相互独立(independent);如果存在\(P(x,y\vert z)=P(x\vert z)P(y\vert z)\),则称这两个随机变量在给定\(z\)时条件独立(iconditionally ndependent)。
进一步地,从条件概率的定义稍加推导便可以得出贝叶斯规则(Bayes’ rule):
\[P(x\vert y)=\frac{P(x)P(y\vert x)}{P(y)}\]期望、方差和协方差
顾名思义,期望(expectation)描述的是某个函数在其相应概率分布下的平均值(最有可能、最为期望出现的值),同样地,可由积分(求和)得出:
\[E[f(x)] = \int p(x)f(x)dx\]方差(variance)被用于衡量对\(x\)依据概率分布采样时,其函数值可能呈现出多大的差异:\(Var(f(x)) = E[(f(x)-E[f(x)])^2]\),其平方根被称为标准差(standard deviation)。
协方差(covariance)则描述了两个变量线性相关性的强度:
\[Cov(f(x), g(y)) = E[(f(x)-E[f(x)])(g(y)-E[g(y)])]\]协方差的绝对值较大意味着它们都距离自己的期望值较远,类似的指标如相关系数(correlation)则将每个变量的贡献归一化,如此一来只衡量变量之间的相关性而不受尺度大小的影响。需要注意的是,协方差和相关性有联系,但实际不同,存在相互依赖但协方差为零的情况,不过可以说明的是在该情况下,变量之间不存在线性关系。另外,协方差矩阵(covariance matrix)是一个\(n\times n\)的方阵,满足\(Cov(x)_{i,j} = Cov(x_i,x_j)\),可以看出,其对角元即为方差。
常见的概率分布
Bernoulli分布(Bernoulli distribution)是一个二值随机变量分布,即对于\(\phi \in [0,1], P(x=1)=\phi, P(x=0)=1-\phi\),所以有,\(E[x]=\phi, Var(x)=\phi (1-\phi)\)。
Multinoulli分布(Multinoulli distribution)是指k个状态的离散型随机变量分布,即对向量\(p \in [0,1]^{k-1}\)参数化,每一个分量\(p_i\)即表示第i个状态的概率,最后的第k个状态可以由\(1-\sum_i^{k-1}p_i\)得出。这两个分布是常见的对有限状态进行枚举建模的离散型变量概率分布,不过在真正数学应用或者大数据建模中,遇到更多的还是连续型变量。
高斯分布(Gaussian distribution),即正态分布(normal distribution),公式、曲线如下:
\[N(x; \mu , \sigma^2) = \sqrt{\frac{1}{2\pi \sigma^2}}exp(-\frac{1}{2\sigma^2}(x-\mu)^2)\]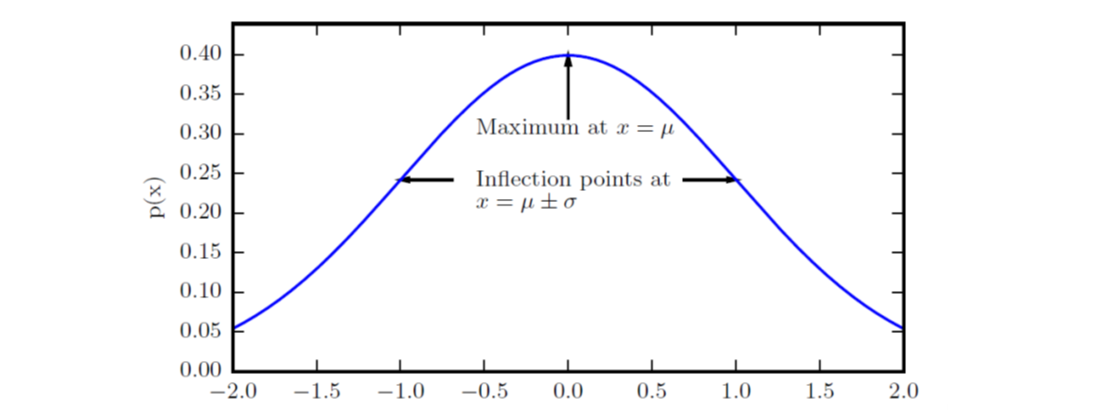
当\(\mu=0,\sigma=1\)时称为标准正态分布,中心峰值的x轴坐标为其期望值,即\(E[x]=\mu\),方差则为\(\sigma^2\)。在很多时候,正态分布都是最好的选择:首先,中心极限定理说明很多独立随机变量的分布都近似于正态分布,很多实际的信号数据可能是各种正态分布的叠加;其次,在具有相同方差的所有可能的概率分布中,正态分布具有最大的不确定性,也意味着其带来的先验知识最少。另外,把正态分布推广到多维空间则具有如下定义:
\[N(x; \mu , \Sigma) = \sqrt{\frac{1}{(2\pi)^n det(\Sigma)}}exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))\]此时的\(\mu\)为向量,表示每个维度上的均值,\(\Sigma\)则为分布的协方差矩阵。
指数分布(exponential distribution)利用一个指示函数1_{x\ge 0}来使得\(x\)取负数时概率为零,因而这是一个当\(x=0\)时取得边界点的分布:
\[p(x; \lambda) = \lambda 1_{x\ge 0}exp(-\lambda x)\]拉普拉斯分布(Laplace distribution)允许我们在任意一点\(\mu\)处设置峰值,要注意当\(\mu=0\)时,它的正半部分正好是指数分布的一半:
\[Laplace(x; \mu, \gamma) = \frac{1}{2\gamma}exp(-\frac{\vert x-\mu \vert}{\gamma})\]Dirac分布(Dirac distribution)使用了一个特殊的\(\delta\)函数,其在除零点外的所有点的值都极限趋于0,但积分为1,这种依据积分性质定义的函数称为广义函数。Dirac分布常定义为在\(\mu\)处无限窄也无限高的形式:
\[p(x) = \delta(x-\mu)\]实际中遇到的情况往往可能是多种分布的混合形式,即混合分布(mixture distribution),这同时也是利用简单概率分布生成复杂分布的一种策略,比如:
\[P(x) = \sum_i P(c=i)P(x\vert c=i)\]其中\(P(c)\)是各组件的一个Multinouli分布。这里就要注意一个概念:潜变量(latent variable),它指的是我们不能直接观测到的随机变量,如上述式中的变量\(c\)。一个常见的混合分布是高斯混合模型(Gaussian Mixture Model),它的组件是带有不同参数的高斯分布,任何平滑的概率密度都可以用有足够多组件的高斯混合模型以任意精度来逼近。
概率分布中常见的函数
logistic sigmoid函数的范围是\((0, 1)\),常出现在深度学习的模型中,不过该函数当变量绝对值非常大时会出现饱和现象,对输入的微小改变不敏感:
\[\sigma(x) = \frac{1}{1+exp(-x)}\]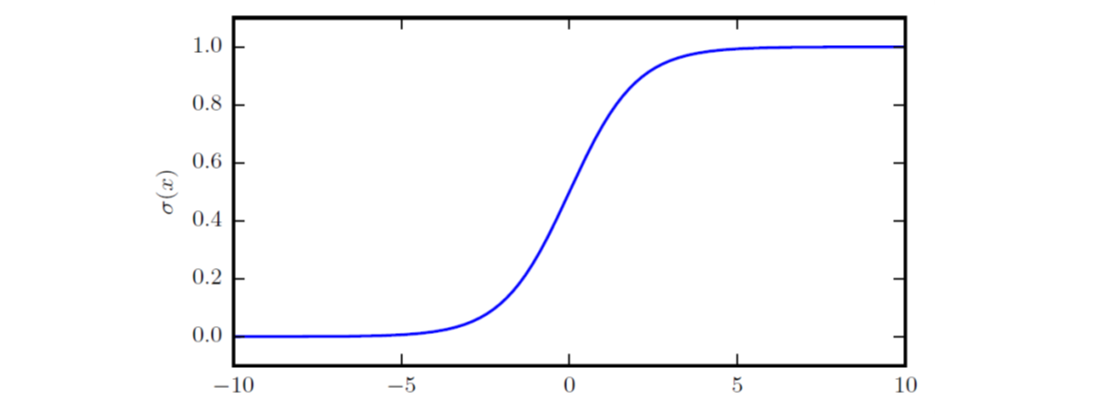
softplus函数的范围是\((0, \infty)\),可用于产生正态分布的\(\sigma\)参数:
\[\zeta(x) = log(1+exp(x))\]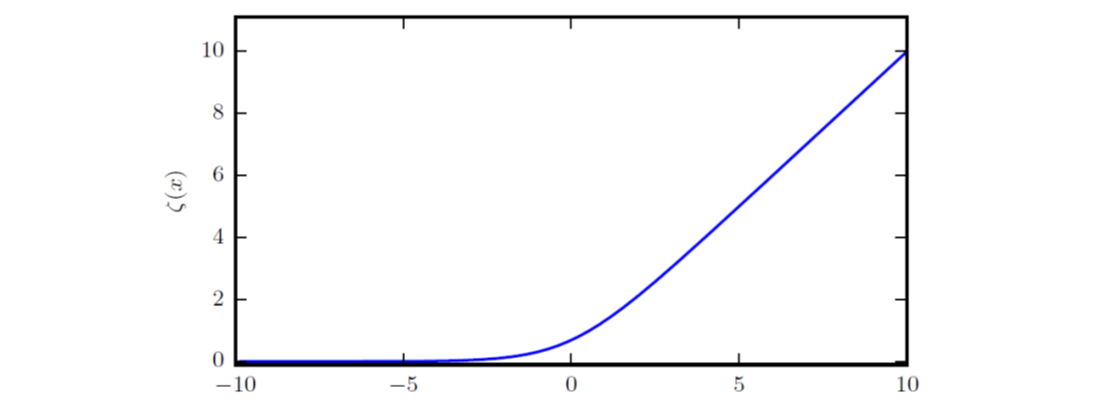
有意思的是,\(\frac{d}{dx}\zeta(x) = \sigma(x)\)
信息论
信息论是电子工程等诸多学科的基础,通过对信号所包含的信息进行量化研究,以设计信息传递的最优编码、设定特定概率分布的数值采样等。信息论的一些思想与概率分布存在相似性,比如我们以下述性质来量化信息:
- 事件发生的可能性越高,其所含的信息量就越少,在某些极端情况下定能发生的事件几乎不含有信息量。
- 独立事件应具有增量的信息。例如,投掷的硬币两次正面朝上传递的信息量,应该是投掷一次硬币正面朝上的信息量的两倍。
基于上述性质可以定义自信息(self-information)的概念:\(I(x) = -logP(x)\)。若以自然常数为底数,则单位为奈特(nat),1 nat即是以\(\frac{1}{e}\)的概率观测到一个事件时获得的信息量。其它还有以2为底数的,其单位为比特(bit)或香农(shannon)。
自信息针对的是单个事件,对于整个概率分布中的总量,可以用香农熵(Shannon entropy)进行量化:\(H(x) = E[I(x)] = -E[logP(x)]\)。可见,香农熵描述了某个分布所产生的期望信息总量,确定性越高则熵越低,一个二值随机变量的香农熵如下图所示:
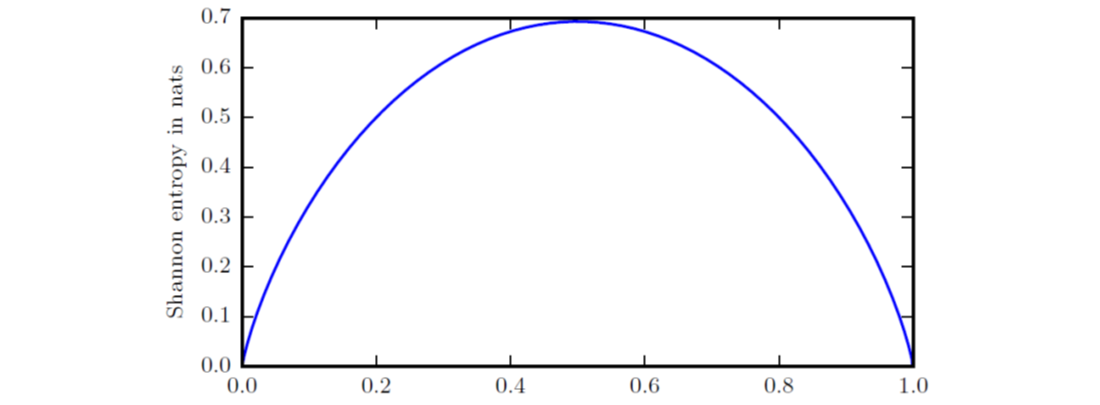
如果随机变量\(x\)有两个单独的概率分布\(P(x)\)和\(Q(x)\),为衡量这两个分布的差异,可使用KL散度(Kullback-Leibler divergence):\(D_{KL}(P\vert \vert Q) = E[log\frac{P(x)}{Q(x)}] = E[logP(x)-logQ(x)]\)。
结构化概率模型
机器学习算法经常涉及到多个随机变量的概率分布,而单个函数很难描述整个联合概率分布,因此可以考虑将其分解成多个因子的乘积形式以减少参数。我们利用“图”的概念来表示这种分解形式并称之为结构化概率模型(structured probabilistic model)或图模型(graphical model)。图的每个节点对应一个随机变量,边表示两个随机变量之间存在直接关系,另外,对于图,存在有向和无向两种模型。
有向(directed)模型用条件概率来表示分解,影响\(x_i\)的条件概率即其父节点,记为\(P_{\alpha G}(x_i)\),因而有\(p(x)=\prod_i p(x_i \vert P_{\alpha G}(x_i))\)。下图是个例子,对应的概率分布可以分解为:\(p(a,b,c,d,e)=p(a)p(b\vert a)p(c\vert a,b)p(d\vert b)p(e\vert c)\)。
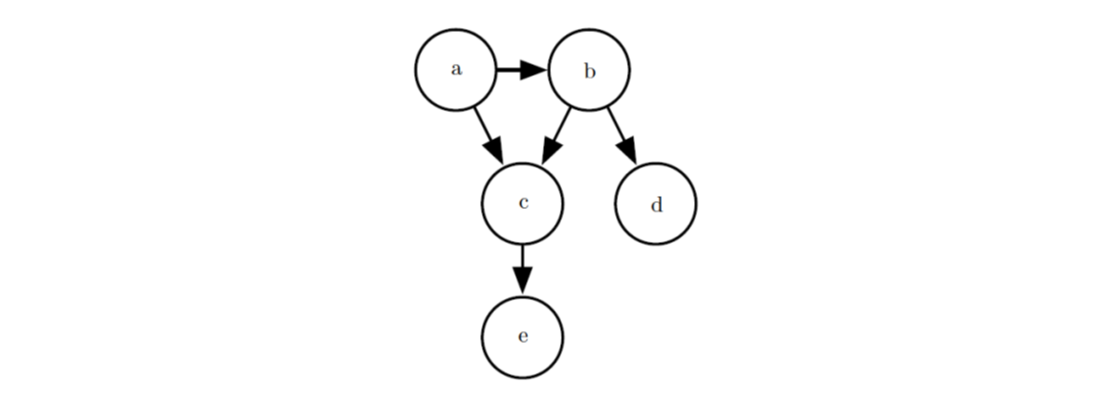
无向(undirected)模型用一组函数(通常不是概率分布)来表示分解,我们将图中两两之间存在边的节点的集合称为团,每个团定义一个非负的函数\(\phi^{(i)}(C^{(i)})\),相应的概率分布为\(p(x)=\frac{1}{Z}\prod_i \phi^{(i)}(C^{(i)})\),其中\(Z\)的作用是归一化。利用上图作为例子,对应的概率分布可以分解为:\(p(a,b,c,d,e)=\frac{1}{Z} \phi^{(1)}(a,b,c) \phi^{(2)}(b,d) \phi^{(3)}(c,e)\)。

